Let us continue our visit to classical mechanics.
We have discussed the action principle as it applies to a single
particle moving in one and three dimensions.
Now consider the mechanics of a violin string, which is allowed to vibrate
up and down (but not sideways) while tied at its ends.
An element of the string is denoted by its coordinate x along the string,
and in its motion it is displaced in a direction transverse to the string
by a distance 
.
Now the function 
constitutes an infinite set of coordinates for
which x is the index.
(Recall the correspondence 
in Section 1.)
A function of space and time is a trajectory of the entire
string.
It is not hard to show that the kinetic and potential energies of the string
are given by
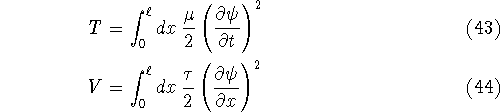
where 
is the length of the string; 
is its density (mass per unit
length); and 
is the tension of the string.
As before L=T-V, and thus the action is
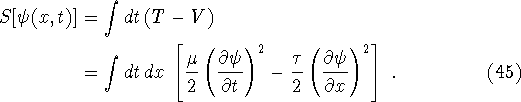
This is of the form
and so the Euler-Lagrange equation is [cf. (28)]
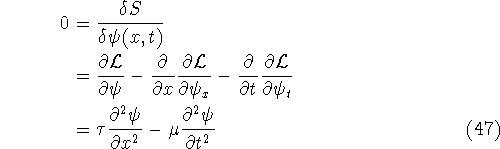
This partial differential equation is the wave equation,
where we identify the wave velocity as 
.
The string is the simplest example of a problem in continuum
dynamics, also called classical field theory.
is the field, a variable associated with each point in
space that evolves dynamically in time.
(Think of the electric field, governed by Maxwell's Equations.)
S is the action for the field theory, and the wave equation is the
equation of motion, which is a partial differential equation because
of the added element of x-dependence.
For any trajectory , the energy is the sum of the kinetic
and potential energies,
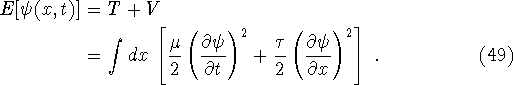
Note that there is no integral over time in defining the energy. One might be interested in finding the time-independent shape of the string that minimizes the energy. Here the kinetic energy is zero, and one minimizes the functional
The Euler equation here is
which gives the trivial solution (satisfying the boundary conditions)
.
This is also obvious from the form of (50).
It is of course easy to invent an energy-minimization problem with
a non-trivial solution.
The point of this exercise is to show that the same problem might invite
both time-dependent and time-independent variational calculations.
Of course, not all field theory problems are one-dimensional like the
vibrating string.
Examples of two-dimensional field theory are the vibrations of a drumhead
or surface waves in water, where the physics is described by a function
and an action functional
.
Electromagnetism is a three-dimensional field theory, with six separate
fields that are the components of 
and 
.
