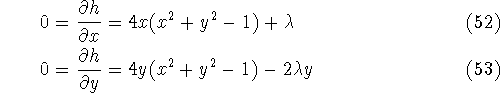
These two equations, together with the constraint ![]() , give
three equations for the three unknowns x, y, and
, give
three equations for the three unknowns x, y, and ![]() .
.
Frequently a minimization problem includes a constraint. In ordinary multivariable calculus, for instance, one might be asked to find the minimum of f(x,y,z) under the constraint that g(x,y,z)=0. This is usually done by the method of Lagrange multipliers.
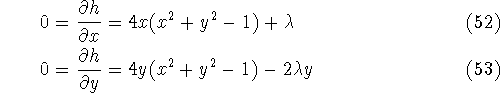
These two equations, together with the constraint ![]() , give
three equations for the three unknowns x, y, and
, give
three equations for the three unknowns x, y, and ![]() .
.
If there is more than one constraint, we use more than one Lagrange multiplier, one multiplier for each constraint.
Constrained minimization of a functional is no different.
To minimize S[y(x)] under the constraint T[y]=0, define the combined
functional ![]() .
Then write the minimization equation
.
Then write the minimization equation
This will yield an equation for y(x) as always, with ![]() appearing
as a parameter.
The constraint equation T[y]=0 gives another equation, so that there
is enough to fix
appearing
as a parameter.
The constraint equation T[y]=0 gives another equation, so that there
is enough to fix ![]() , too.
, too.
![]()
This has the general solution ![]() .
Plugging this into the constraint gives
.
Plugging this into the constraint gives
![]() .
Solving this equation together with the boundary conditions gives
.
Solving this equation together with the boundary conditions gives
![]() ,
, ![]() , and
, and ![]() , so the solution is
y=6x(1-x).
, so the solution is
y=6x(1-x).
If there is more than one constraint, say ![]() and
and ![]() , then
we use two Lagrange multipliers and we minimize
, then
we use two Lagrange multipliers and we minimize
![]() .
.
A more complex problem is that of a locally constrained
minimization.
Here there is typically a functional of (at least) two
functions, S[x(t),y(t)], along with an equation that constrains
x(t) and y(t) at every time t.
Since there are an infinite number of constraints--one at every
time t--there must be an infinite number of Lagrange multipliers--one at
every time t.
So we have a Lagrange multiplier function ![]() .
If the constraint is f(x(t),y(t))=0 then we define the new functional
.
If the constraint is f(x(t),y(t))=0 then we define the new functional
![]()
When we minimize R with respect to x(t) and y(t), we get differential
equations in which the unknown function ![]() appears.
In addition, the algebraic equation f(x(t),y(t))=0 is available to help
fix
appears.
In addition, the algebraic equation f(x(t),y(t))=0 is available to help
fix ![]() .
.
![]()
and the constraint is ![]() .
We define
.
We define
![]()
the minimization of which gives the Euler-Lagrange equations
![]()
![]()
Since in these differential equations ![]() is an unknown function,
their solution is quite difficult.
is an unknown function,
their solution is quite difficult.
The example shows that the Lagrange multiplier method for local constraints is not really a calculational tool. It is, however, very important as a conceptual device in the analytical mechanics of constrained systems, and reappears in classical and quantum field theory.