which just evaluates its argument y(x) at the specific
point 
. What is its functional derivative 
?
F only depends on the value of y at
, so if we vary y at some
other place, F will be unchanged.
Thus
If we change y exactly at
, however, F obviously changes.
An easy way to proceed is to rewrite (61)
as an integral functional. Let's say there is some function 
that allows us to write
What are the properties of 
? Since F[y] has no dependence on y(x) for 
, we clearly have
(64)
What is
at 
? If it were finite, the integral (63)
would always be zero, because of the infinitesimal measure dx. Thus
must be infinite at
!
The actual value of 
will never really concern us. All we have to know is how to integrate with
. In fact, we can take the following [which is just (61)
and (63)] to be the definition
of
:
In view of (63), we can state the following result, which must be used with care:
or, more compactly,
Properly speaking,
is not a function at all, since its infinite value takes us out of the
usual domain of definition of functions. Mathematicians call it a distribution,
a limit of a sequence of functions that really only has meaning in integral
expressions such as (65). Let us evaluate
(65) for the special case y(x)=1,
choosing as well 
. We get
So the area under the 
function is 1 (even though its width is zero!). One possible realization
of
as a sequence of functions is the set of gaussians
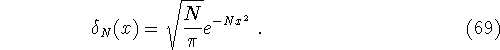
Each 
has unit area, and
becomes higher and narrower as 
. Mathematicians will always be careful to insert 
into integrals like (65) and to evaluate
the integral before taking the
limit.
Expressions such as (67) have meaning
only when they are multiplied by some function of
and integrated over
; then we are returned to the usual kind of functional derivative. At a
physicist's level of rigor, however, (67)
can be used to deal with chain rules and with higher functional derivatives,
taking care to remember that the limit
may contain pitfalls.
