The Euler equation

When the functional is a simple integral, Euler's equation gives a powerful formula for quick calculation of the functional derivative. Start with the case

 

i.e., a simple integral where the integrand is some function of x and y(x). Varying y(x),

where in the second equality we have again thrown away terms of order and higher. Referring to the definition (5), we find

 

Eq. (18) is a handy formula that is applicable whenever the functional is of the form (16).

Example.

For , eq. (18) gives the result .

Euler's formula is not (18), but rather applies to a case somewhat more complicated. Consider the case where the integrand L contains both y and y'=dy/dx,

 

A variation of y(x) by some specific gives

where is the derivative of the small variation . Expanding to first order in and its derivative,

 

Note that we have differentiated L(x,y,y') as if y and y' are unconnected, independent variables. This is not as confusing as it sounds.

Example.

If , then , , and .

Eq. (21) is not yet in the form of (5) so we cannot yet extract the functional derivative. The problem is to turn into in the last term; we do this with an integration by parts:

 

The first term on the right hand side of (22) is a boundary term: It is proportional to the values of at the boundaries of the interval [a,b]. Using (22) in (21), we obtain

  (23)

Now we can compare to (5) and conclude that

 

as long as x is not at a boundary of the interval; if x is at a boundary, there is an added term that can be read off (23). This is Euler's formula, an extremely useful short cut to the functional derivative when the functional is of the form (19).

Simple generalizations of Euler's formula:

1. The integrand L can contain higher derivatives of y(x). The extension of Euler's equation is derived in the same way as (24).

   Example.

   If

   

   then

   

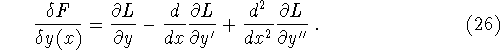
   The second derivative comes from the need to integrate by parts twice to deal with , and two minus signs make a plus sign.

2. If the argument of the functional is a function of more than one variable, then partial derivatives can appear in L.

   Example.

   Let

   

   where we use the notation , etc. Then

    

Examples of the use of Euler's formula can be found in the next section.