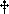Consider a function F(y).
You can differentiate it, 
.
Then if you start at a point 
and you move
a distance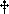
dy, the function F changes by an amount
.
Now consider a function of several variables, 
, 
, 
.
Writing the function as 
, it has partial derivatives
, 
, .
If I start at a point 
, 
, and move to a new point
via a displacement 
, 
, , the function F will
change according to
.
Defining 
, where
dx, dy, and dz are independent step sizes, we have
We can write the independent variables , ,
collectively
as 
(n=1, 2, ).
y then looks like a function of the integer variable n.
F is thus a function of the function y.
But a function y(x) in physics usually depends on a variable
x that takes on all real values in some interval [a,b].
To relate this to what we have discussed so far, let's choose
N points on the interval [a,b] with the points a distance
apart, where 
.
The 
point is at 
.
We can represent the function y(x) by its values on the N points,
so that we consider the function 
, which
would give more and more information about the original y(x) as
, 
.
We can define a function of all the 
, namely 
.
In the limit , the function F becomes a function of the
function y(x).
We then call F a functional of y(x), written F[y].
It is a function of all the values of y(x) in the interval
[a,b]: an infinite number of independent variables!
A functional takes as input a function y(x) on a domain--not the value of the function at a specific point x, but all the values of y at all the x's in the domain. Its output is a number.
. Then
and 
.
F depends on the entire functional form of y(x) in the interval
[0,1].
and 
.
If we change the values of , the function will
change
according to (1).
Let's rewrite this as
How does this look in the limit?
Recall the definition of an integral:
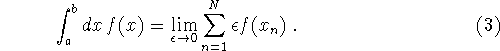
Rewrite (2) as
Taking the limit , with 
,
and introducing the notation 
,
(4) becomes
Here 
is the particular function y(x) that is the starting
point for the arbitrary infinitesimal change 
.
The 
has been absorbed into 
; this
can be taken to be the definition of the functional derivative
.
The meaning of (5) is the same as the meaning of (1).
The change in F is a sum of terms proportional to the infinitesimal
changes , with constants of proportionality that are just
the functional derivative (i.e., the partial derivatives)
.
You can think of this derivative as giving the response of the
functional
F to a small change in y, with the change localized at x.
The preceding discussion gives a definition of the functional
derivative,
but it does not give a useful method for calculating it since for each
problem we would have to define carefully a mesh of points 
and
a function F of the discrete set 
.
More usually, we have a functional F[y], defined for
functions y of a continuum variable x,
and we need its functional derivative.
We can start with (5) as a definition of the functional
derivative, and use it to calculate.
To calculate the functional derivative, we calculate the change dF
that is due to an infinitesimal change in the independent
variables:
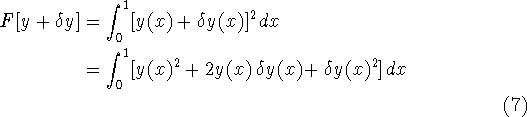
Now we throw away 
, since 
is
an infinitesimal and we have in mind the 
limit.
Thus to first order in ,
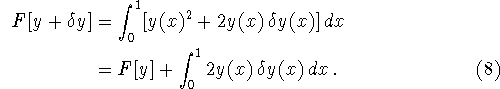
The infinitesimal change in F due to is then
The crucial step is to compare (9) to (5). We thus identify
