Generalizations

1. A functional can depend on more than one function. Then the functional derivative with respect to each argument is defined in the obvious way, each calculated while keeping the other function constant.

   Example.

   If

   

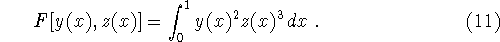
   then

   

2. The independent function can be a function of more than one variable.

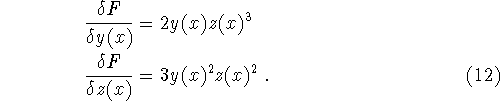
   Example.

   Taking 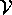to be a specific domain of integration in space, let

   

   Then

   

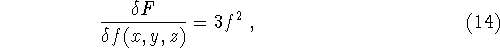
   just as in the one-dimensional case. F can also be written as .

3. A functional doesn't have to be a simple integral.

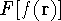   Example.

   Take

   

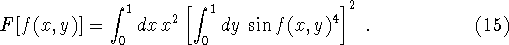
   Here, as always, the definition (5) gives a straightforward method for calculating the functional derivative .
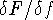