Classical mechanics rests upon Newton's Laws. A central theme in more advanced treatments (called analytical mechanics) is the connection of Newton's Laws to an action principle. Mathematically, this is a simple application of what we have developed above.
Take a single particle that is free to move along a line, under the influence of a force derivable from a potential. If x(t) is the coordinate of the particle, then its kinetic energy is
where we use the notation 
for the velocity.
The potential energy is V(x), so that the force acting on the particle
is 
.
Given the position x and velocity 
of the particle at any given
time, we can define a new function called the Lagrangian,
Now consider the following boundary value problem:
Given that the particle is known to be at position 
at time 
,
and at some other position 
at a later time 
, where was the
particle at the times in between, that is, what is the function x(t)--the
trajectory--for
?
According to Hamilton, we begin by defining the action of a trajectory
as the following functional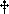
of x(t):
Hamilton's Principle of Least Action states that the true trajectory x(t) is that function that minimizes the action (31).
How does one minimize a function y(x)? One looks for points where its derivative vanishes. How does one minimize a functional? The same! Hamilton's Principle can be written as
for all .
The action S is precisely of the form (19), where Euler's formula
applies, so (32) is equivalent to
This is called the Euler-Lagrange equation of the action (31),
or simply the Lagrange equation.
Let's show that this really works. Inserting the Lagrangian (30) into the Lagrange equation (33), we obtain
which is just F=ma.
This is a second-order ordinary differential equation for x(t).
To complete the minimization of the action, one must solve (34) for
x(t) (this is the hard part!) to get a solution containing two arbitrary
constants; then these constants are fixed by the boundary values
and 
.
This was a rather trivial example, but it does constitute a proof (in reverse) of Hamilton's Principle for this simple case. The real power of the Lagrangian method as derived from Least Action can only be felt when the mechanical system is complex, and we leave this to a course in Analytical Mechanics.
It should be noted that setting 
does not necessarily
lead to a minimum of the action.
It could just as well be a maximum or a saddle point, depending on the signs of
the second derivatives at the solution.
Fortunately, Hamilton's Principle, while it is often called the Principle
of Least Action, does not really require a minimum of S but only a
stationary point, which means that any solution of
will do.
As we have seen, this is just what gets us back to Newton's Second Law,
which is all that is needed.
This example, Hamilton's Principle in mechanics, shows the most common application of functional differentiation, namely, finding the minimum (or at least a stationary point) of a functional. Hamilton's Principle is but one example of a variational principle, a theme which recurs in many fields of physics. In optics one has Fermat's Law of Least Time; in quantum mechanics one has the Rayleigh-Ritz variational method and Schwinger's action principle; and in classical mechanics there are other forms of Least Action in other contexts. Most mathematics textbooks discuss functional methods with these applications in mind, so they treat only the minimization problem and not the wider range of application of functional differentiation. The most common name for this subject in the textbooks is calculus of variations.
A slightly more complex case is that of a particle free to move in three
dimensions, so that it has three coordinates 
.
Then the action is a functional of the three functions x,y,z,
The Lagrange equations come from varying separately with respect to x, y, and z,
with another equation for y(t) and another for z(t). The three equations can be summarized as
The first 
is just the ordinary gradient, containing derivatives
with respect to the components of r; the second contains
derivatives with respect to the components of 
:
Then
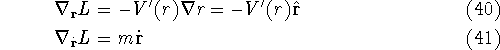
and so the Lagrange equations are
Of course, the problem can also be done component by component, using (36) and its siblings.
